Filament Games stays connected to the scholarly side of game-based learning (GBL) through our GBL Luminaries Program. Academics in the Luminaries program work with our staff to maintain a healthy dialogue between game-based learning theory and practice through all-staff lectures and guest blog posts. Today’s GBL Luminary guest post is from Douglas B. Clark, Werklund Professor of Design-Based Learning and the Learning Sciences at the University of Calgary. Formerly a high school and middle school science educator, Dr. Clark’s research focuses on students’ and teachers’ design and learning processes, primarily in the context of technology-enhanced environments, as well as designing simulations, games, and multimedia inquiry environments for science learning (e.g., http://www.surgeuniverse.com).
Intrinsic, Endogenous, Disciplinarily-Integrated, Conceptually-Integrated, or Objects to Think With? What is Academically Meaningful Play?
Douglas B. Clark, Jesus Enrique Hernandez Zavaleta, & Sandra Becker
University of Calgary
Over the years, many games researchers have explored ideas around the relationship between game mechanics and educational learning goals. Most often, these explorations have focused on questions of what it means for the educational learning goals to be intrinsic or endogenous to the game mechanics (e.g., Habgood & Ainsworth, 2011; Kafai, 1996). Habgood, Ainsworth, and Benford (2005), for example, define intrinsic design as:
- Intrinsically integrated games deliver learning material through the parts of the game that are the most fun to play, riding on the back of the flow experience produced by the game and not interrupting or diminishing its impact.
- Intrinsically integrated games embody the learning material within the structure of the gaming world and the player’s interactions with it, providing an external representation of the learning content that is explored through the core mechanics of the gameplay. (p. 173)
Note that this framing of intrinsic design differs somewhat from the proposals of scholars such as Lepper and Malone (1987) who define intrinsic more specifically in terms of intrinsic motivation. Habgood et al.’s framing of intrinsic integration focuses on the location and relationship of the learning mechanics with regard to the game mechanics that are the most engaging, whereas extrinsic design involves a separation between the game elements that are most engaging to the player and the game elements that were most central to the educational learning goals. Math Blaster (Davidson & Associates, 1983), where students answer academic questions in one part of the game in order to be able to blast space trash in a completely separate part of the game, is probably the most famous and iconic example of extrinsic design.
Through a series of research projects, our extended group of colleagues has explored various refinements to these ideas of intrinsic/endogenous design across multiple funded research projects. Our earlier work focused on “conceptually-integrated” games (Clark & Martinez-Garza, 2012) where the focal science concepts are integrated directly into the core mechanics of the game and are the means through which the player navigates and transforms the game-world (e.g., core mechanics around manipulating physics concepts to move through the world). Conceptually-integrated games are juxtaposed with conceptually-embedded games, where science processes are embedded within the game world but are not central to actually navigating the game world (e.g., traveling around in a 3D world to reach locations where data can be collected).
We then pushed deeper by exploring ideas around “disciplinarily-integrated games” that specifically focus game-mechanics on transforming, developing, and interpreting disciplinary representations and inscriptions (Clark, Sengupta, Brady, Martinez-Garza, & Killingsworth, 2015; Clark, Sengupta, & Virk, 2016; Clark & Sengupta, 2020; Sengupta & Clark, 2016). Disciplinarily-integrated games build on the idea that interpreting, translating, and manipulating across formal representations is central to scientific practice (Duschl, Schweingruber, & Shouse, 2007; Lehrer & Schauble, 2006, 2007; Pickering, 1995). Examples of these games might be developed inside Cartesian graphs, force body diagrams, computer code, or other formal disciplinary inscriptions or representations.
We have not been alone in these explorations. Other research groups, such as Holbert and Wilensky (2019) with their CART and objects-to-think-with perspectives, have also investigated similar relationships. Whereas all of these perspectives have asked questions about the location and nature of learning goals in relationship to core game mechanics in a game, our current research project has raised another question that is salient to all of these perspectives. What is academically meaningful play, and what is the relationship of academically meaningful play to these various perspectives on intrinsic/endogenous game design?
Our current funded project focuses on how the design of learning activities affects what aspects of the learning goals are forefronted in terms of mathematical and computational thinking and learning. As a bit of background, learning about geometric transformations is challenging for students since the transformations are intended to be understood as mapping of the whole plane, using the “mapping” metaphor more as a mathematician might (Edwards, 2003; Lakoff & Núñez, 2000). Yet, students tend to think about geometric transformations in terms of a “motion” metaphor that draws upon their embodied understandings (e.g., Authors, in prep; Edwards, 2003; Hollebrands, 2003; Yanik & Flores, 2009). The question arises how both of these very productive and useful understandings contribute to thinking about geometric transformations in the “mapping” metaphor.
Figure 1. Transformations Quest (https://mathgame.ucalgary.ca)
The game we developed, and are continuing to refine, as part of this research is called Transformations Quest (https://mathgame.ucalgary.ca, see Figure 1). There are already games that engage students with geometric transformations on Cartesian planes, with the NCTM’s (n.d.) Flip-N-Slide game being a prime example (Figure 2), along with many others such as Transformation Golf 2 (Hoodamath, n.d.), and Transtar (Mangahigh, n.d.). Thus, the idea of building a game about geometric transformations on a Cartesian plane is not what is novel about this research project. Instead, the focus is on how the game might be designed using the students’ motion understandings to develop the mapping aspects of geometric transformations, which the other games we found seemed to do less well, and to propose design principles to support such outcomes.
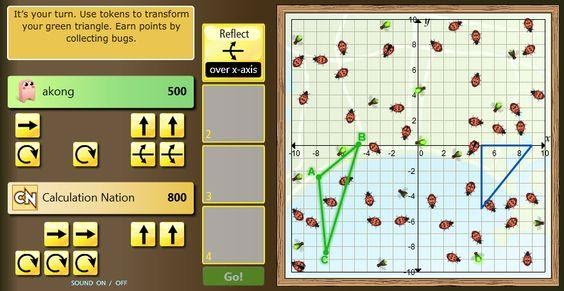
Figure 2. NCTM’s Flip-N-Slide (which unfortunately was taken down from their site in January 2021 with Adobe Flash’s decision to no longer support Adobe Flash Player)
As a point of comparison, we might compare Transformation Quest with Flip-N-Slide. Interestingly, NCTM’s Flip-N-Slide and our game have many similarities. Players specify a sequence of transformations by dragging blocks representing transformation commands into a series. Transformation commands include translations, reflections, and rotations on a Cartesian plane. The player can specify the direction and magnitude of each command. When the player clicks on the “run” button, a triangle on the screen follows those commands. In fact, both games have designs that are intrinsic, endogenous, conceptually integrated, and disciplinarily integrated according to the definitions above. Thus, addressing only these framings is not sufficient to distinguish between the two games. That is why we propose that we need to think more about academically meaningful play.
More specifically, while we were impressed with how fun and engaging Flip-N-Slide is to play, and we liked the basic idea of building a game about geometric transformations into Cartesian coordinates as Flip-N-Slide does, it seemed clear to us that key aspects of the design might be more effective in helping students come to think about transformations in terms of mapping perspectives because the meaningful choices in Flip-N-Slide are not academically meaningful choices.
For our current thinking, we want to draw and extend upon ideas about meaningful play from game design (Salen & Zimmerman, 2005) to focus specifically on mathematical meaning (or academic meaning more generally). According to Salen and Zimmerman, “meaningful play emerges from the interaction between the players and the system of the game, as well as from the context in which the game is played” (p. 60). From this perspective, a game is a system of elements, possible actions, and relationships between those elements and actions. This system of elements, actions, and the relationships between them is defined by the rules of the game and the design of the game. One way of viewing what a player does during a game is in terms of making choices. When a player makes a choice within the game, that choice changes the state of the system within the game. Choices and decisions are meaningful in a game if the results of those choices are: (a) discernible to the player in the sense that the ramifications of the choice are communicated to the player and (b) integrated into the ongoing game in an impactful way.
For academically meaningful play, we extend these definitions by specifying that the decisions and choices must also be academically meaningful (in our case mathematically and computationally) at both the disciplinary as well as the classroom levels. As Gadanidis et al. (2018) explain, “The traditional – the easy – way of engaging young children with big mathematical ideas is to fragment the ideas to an extent that the mathematical structure is lost” (p. 34). The challenge in designing games for academically meaningful play is to structure the game so that players, in attending to singular mathematical concepts, do so in the context of the larger mathematical composition, thereby avoiding “mathematical structure giv[ing] way to fragments of mathematics” (Gadanidis et al., 2018, p. 34). We claim that this challenge also extends to other STEM disciplines and beyond. In academically meaningful play, our goal is to focus gameplay on meaningful choices that keep the larger academic (in our case mathematical) ideas intact while simultaneously meeting the goals and needs of teachers and students in classrooms. We are still in the early days of this research and our thinking, but we wanted to share these initial thoughts and the link to our game with everyone in hopes of starting a conversation and getting feedback!
Acknowledgement
This material is based upon work supported by the National Science Foundation under Grant No. 1742257. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
References
Clark, D. B., & Martinez-Garza, M. (2012). Prediction and explanation as design mechanics in conceptually-integrated digital games to help players articulate the tacit understandings they build through gameplay. In C. Steinkuhler, K. Squire, & S. Barab (Eds.), Games, learning, and society: Learning and meaning in the digital age (pp. 279-305). Cambridge University Press. https://doi.org/10.1017/CBO9781139031127.023
Clark, D. B., & Sengupta, P. (2020). Reconceptualizing games for integrating computational thinking and science as practice: Collaborative agent-based disciplinarily-integrated games. Interactive Learning Environments, 28(3), 328-346. https://doi.org/10.1080/10494820.2019.1636071
Clark, D. B., Sengupta, P., & Virk, S. S. (2016). Disciplinarily-integrated games: Generalizing across domains and model types. In D. Russell and J. Laffey (Eds.), Handbook of research on gaming trends in P-12 education (pp. 178-194). IGI Global. https://doi.org/10.4018/978-1-4666-9629-7.ch009
Clark, D. B., Sengupta, P., Brady, C., Martinez-Garza, M., & Killingsworth, S.* (2015). Disciplinary integration in digital games for science learning. International STEM Education Journal, 2(2), 1-21. https://doi.org/10.1186/s40594-014-0014-4 http://www.stemeducationjournal.com/content/pdf/s40594-014-0014-4.pdf
Davidson & Associates (1983). Math Blaster! http://www.mathblaster.com
Duschl, R. A., Schweingruber, H. A., & Shouse, A. W. (Eds.) (2007). Taking science to school: Learning and teaching science in grades K-8. National Research Council Board on Science Education, Center for Education, Division of Behavioral and Social Sciences and Education. The National Academies Press.
Edwards, L. (2003). The nature of mathematics as viewed from cognitive science. Europena Research in Mathematics Education III, (pp. 1-10).
Gadanidis, G., Clements, E., & Yiu, C. (2018). Group theory, computational thinking, and young mathematicians. Mathematical Thinking and Learning, 20(1), 32-53. https://doi.org/10.1080/10986065.2018.1403542
Habgood, M. J., & Ainsworth, S. E. (2011). Motivating children to learn effectively: Exploring the value of intrinsic integration in educational games. The Journal of the Learning Sciences, 20(2), 169-206.
Habgood, M. P. J., Ainsworth, S., & Benford, S. (2005a). Endogenous fantasy and learning in digital games. Simulation & Gaming, 36, 483–498.
Holbert, N., & Wilensky, U. (2019). Designing educational video games to be objects-to-think-with. Journal of the Learning Sciences, 28(1), 32-72.
Hollebrands, K. (2003). High school students’ understandings of geometric transformations in the context of a technological environment. Journal of Mathematical Behavior, 22, 55-72. https://doi.org/10.1016/S0732-3123(03)00004-X
Hoodamath (n.d.) Transformation Golf 2. https://www.hoodamath.com/
Kafai, Y. B. (1996). Learning design by making games: Children’s development of strategies in the creation of a complex computational artifact. In Y. B. Kafai & M. Resnick (Eds.), Constructionism in practice: Designing, thinking and learning in a digital world (pp. 71–96). Erlbaum.
Lakoff, G., & Núñez, R. (2000). Where mathematics comes from: How the embodied mind brings mathematics into being. Perseus Books Group.
Lehrer, R., and Schauble, L. (2006). Cultivating model-based reasoning in science education. In R.K. Sawyer (Ed.), The Cambridge Handbook of the Learning Sciences (pp. 371-388). Cambridge University Press.
Lehrer, R., and Schauble, L. (2007). Scientific thinking and science literacy: Supporting development in learning in contexts. In W. Damon, R.M. Lerner, K.A. Renninger, & I.E. Sigel (Eds.), Handbook of child psychology: Child psychology in practice (6th ed., Vol. 4, pp. 53-196). Wiley.
Lepper, M. R., & Malone, T. W. (1987). Intrinsic motivation and instructional effectiveness in computer-based education. In R. E. Snow & M. J. Farr (Eds.), Aptitude, learning and instruction: Cognitive and affective process analyses (Vol. 3, pp. 255–286). Erlbaum.
Mangahigh (n.d.). Transtar. https://www.mangahigh.com/en-us/games/transtar
NCTM (n.d.) Flip-N-Slide. https://calculationnation.nctm.org/Games/AboutGames.aspx
Pickering, A. (1995). The Mangle of practice: Time, agency, and science. University of Chicago Press.
Salen, K., & Zimmerman, E. (2005). Game design and meaningful play. In J. Raessens & J. Goldstein (Eds.), Handbook of computer game studies (pp. 59-79). MIT Press.
Sengupta, P., & Clark, D. B. (2016). Playing modeling games in the science classroom: The case for disciplinary integration. Educational Technology, 56(3), 16-22. https://arxiv.org/abs/1607.05094 Yanik, H. B., & Flores, A. (2009). Understanding rigid geometric transformations: Jeff’s learning path for translation. The Journal of Mathematical Behavior, 28, 41-57.